THE WORK WITHIN THE WORK

E PLURIBUS UNUM

A set is a Many which allows itself to be thought of as a One.
-GEORG CANTOR
Gesammelte Abhandlungen (1883)

ZERMELO-FRAENKEL-SKOLEM
AXIOMS FOR SET THEORY

  1. AXIOM OF EXTENSIONALITY
    Two sets are equal if and only if they have the same members.
  2. AXIOM OF THE NULL SET
    There exists a set with no members (the empty set).
  3. AXIOM OF UNORDERED PAIRS
    If x and y are sets, then the (unordered) pair {x,y} is a set.
  4. AXIOM OF THE SUM SET OR UNION
    If x is a set of sets, the union of all its members is a set.
  5. AXIOM OF INFINITY
    There exists a set x that contains the empty set, and that is such that if y belongs to x, then the union of y and {y} is also in x.
  6. AXIOM OF REPLACEMENT
    Any property that can be stated in the formal language of the theory can be used to define the set.
  7. AXIOM OF THE POWER SET
    There exists for each x the set y of all subsets of x.
  8. AXIOM OF CHOICE
    If a into B is a function defined for all a in x, then there is another function f(a) for all a in x, and f(a) is also in B.
  9. AXIOM OF REGULARITY
    No set may be a member of itself.


-PHILIP J. DAVIS & REUBEN HERSH
The Mathematical Experience (1981)

RUSSEL'S PARADOX

The most famous is Russell's paradox. Most sets, it would seem, are not members of themselves - for example, the set of walruses is not a walrus, the set containing only Joan of Arc is not Joan of Arc (a set is not a person) - and so on. In this respect, most sets are rather "run-of-the-mill". However, some "self-swallowing" sets do contain themselves as members, such as the set of all sets, or the set of all things except Joan of Arc, and so on. Clearly, every set is either run-of-the-mill or self-swallowing, and no set can be both. Now nothing prevents us from inventing R: the set of all run-of-the-mill sets. At first, R might seem a rather run-of-the-mill invention - but that opinion must be revised when you ask yourself, "Is R itself a run-of-the-mill set or a self-swallowing set?" You will find that the answer is: "R is neither run-of-the-mill nor self-swallowing, for either choice leads to paradox." Try it!
-DOUGLAS R. HOFSTADTER
Gödel, Escher, Bach (1979)



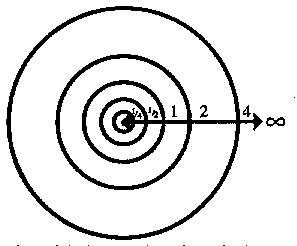The overall image he had of this activity was of two spheres, one expanding outwards towards infinity, and the other contracting in towards zero. The large one grew by continually doubling its size, the smaller shrank by repeatedly halving its size ... and they seemed to be endlessly drawing apart. But with a sudden feeling of freedom and air, Vernor had the conviction that the two spheres were on a direct collision course - that somehow the sphere expanding outwards and the sphere contracting inwards would meet and merge at some attainable point where Zero was Infinity, where Nothing was Everything.
-RUDY RUCKER
Spacetime Donuts (1981)

Thus while the eternal non-being leads toward the fathomless, the eternal being conducts to the boundary.
LAO-TZU
Tao Te Ching (604-666)


MOON                  SUN

UP

BACK NEXT

HOME