HIGHER DIMENSIONS
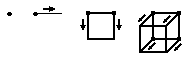
FROM POINT TO CUBE
Start with a point and move it one unit to the right. This produces a one-dimensional line segment. Now move the line segment one unit down the page, producing a two-dimensional square. If we move the square one unit out of the page we get a three-dimensional cube.
Now, we can't really fit a three-dimensional object into the two-dimensional
confines of this page. The standard convention, which
we have used above, is to represent the third dimension as a
direction diagonal to the first two. What if we were to use the
other diagonal direction as the fourth dimension? If we move our
image of the cube one unit in this "fourth dimension," we get a
picture of a four-dimensional hypercube.
-RUDY RUCKER
The Fourth Dimension (1984)
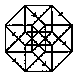
TO HYPERCUBE
This is just the idea given above: to divide space, cuts that are called surfaces are necessary; to divide surfaces, cuts that are called lines are necessary; to divide lines, cuts that are called points are necessary; we can go no further and a point can not be divided, a point not being a continuum. Then lines, which can be divided by cuts which are not continua, will be continua of one dimension; surfaces, which can be divided by continuous cuts of one dimension, will be continua of two dimensions; and finally space, which can be divided by continuous cuts of two dimensions, will be a continuum of three dimensions.
-HENRI POINCARÉ
Science And Hypothesis (1912)
There is a 5th dimension beyond that which is known to man. It is a dimension as vast as space and timeless as infinity. It is the middle ground between light and shadow, between science and superstition, and it lies between the pit of man's fears and the summit of his knowledge. This is the dimension of imagination. It is an area which we call the Twilight Zone.
-ROD SERLING
The Twilight Zone (1959-64) The fact that this dimension remained hidden through the ages, the fact that, even after it made itself felt, it never aroused a habitual and consistent theoretical interest, can (and will) be explained by displaying a peculiar antagonism between the entry into this dimension and the preoccupations involved in all the interests which make up the naturally normal human world-life.
-EDMUND HUSSERL
The Crisis of European Sciences and Transcendental Phenomenology (1937)
Or if it indeed be so, that this other Space is really
Thoughtland, then take me to that blessed Region where I in
Thought shall see the insides of all solid things. There, before
my ravished eye, a Cube moving in some altogether new direction,
but strictly according to Analogy, so as to make every particle
of his interior pass through a new kind of Space, with a wake of
its own - shall create a still more perfect perfection than
himself, with sixteen terminal Extra-solid angles, and Eight
solid Cubes for his Perimeter. And once there, shall we stay our
upward course? In that blessed region of Four Dimensions, shall
we linger on the threshold of the Fifth, and not therein? Ah, no!
Let us rather resolve that our ambition shall soar with our
corporal ascent. Then, yielding to our intellectual onset, the
gates of the Sixth Dimension shall fly open; after that a
Seventh, and then an Eighth...
-EDWIN A. ABBOTT
Flatland (1884)
DEFINITION OF DIMENSION 0
A space X has dimension 0 at a point p if p has arbitrarily small neighborhoods with empty boundaries...
DEFINITION OF DIMENSION n
- The empty set and only the empty set has dimension -1.
- A space X has dimension <= n (n>=0) at a point p if p has arbitrarily small neighborhoods whose boundaries have dimension <= n - 1.
- X has dimension <= n, dim X <= n, if X has dimensions <= n at each of its points.
- X has dimension n at a point p if it is true that X has dimension <= n at p and it is false that X has dimension <= n - 1 at p.
- X has dimension n if dim X <= n is true and dim X <= n - 1 is false.
- X has dimension infinity if dim X <= n is false for each n.
-WITOLD HUREWICZ
& HENRY WALLMAN
Dimension Theory (1941)
| UP | ||||
 |
||||
| BACK |  |
 |
 |
NEXT |
 |
||||
| HOME |