MAPPING DREAMS

PRO & CON

I am free to imagine a horse with or without wings.
-RENÉ DESCARTES
Meditations V (1641)

A horse is a horse for everybody... Representation according to nature is not itself nature; moreover, art is not nature.
-PIET MONDRIAN
Natural Reality and Abstract Reality (1919-1920)

OLD REALITIES IN NEW DREAMS

Bosch, by means of paintings that interfused medieval forms in Renaissance space, told what it felt like to live straddled between the two worlds of the old and the new during this revolution. Simultaneously, Bosch provided the older kind of plastic, tactile image but placed it in the intense new visual perspective. He gave at once the older medieval idea of unique, discontinuous space, superimposed on the new idea of uniform, connected space. This he did with earnest nightmare intensity.

Lewis Carroll took the nineteenth century into a dream world that was as startling as that of Bosch, but built on reverse principles. Alice in Wonderland offers as norm that continuous time and space that had created consternation in the Renaissance. Pervading this uniform Euclidean world of familiar space-and-time, Carroll drove a fantasia of discontinuous space-and-time that anticipated Kafka, Joyce, and Eliot. Carroll, the mathematical contemporary of Clerk Maxwell, was quite avant-garde enough to know about the non-Euclidean geometries coming into vogue in his time. He gave the confident Victorians a playful foretaste of Einsteinian time-and-space in Alice in Wonderland. Bosch had provided his era a foretaste of the new continuous time-and-space of uniform perspective. Bosch looked ahead to the modern world with horror, as Shakespeare did in King Lear, and as Pope did in The Dunciad. But Lewis Carroll greeted the electronic age of space-time with a cheer.
-MARSHALL MCLUHAN
Understanding Media (1964)

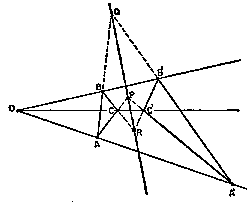
Desargues' Theorem

The pairs of corresponding sides, AB and A'B', BC and B'C', and AC and A'C' of two triangles perspective from a point meet, respectively, in three points that lie on one straight line. With specific reference to our figure the theorem says that if we prolong sides AC and A'C', they will meet in a point P; sides AB and A'B' prolonged will meet in a point Q; and sides BC and B'C' prolonged will meet in a point R. And P, Q, and R will lie on a straight line. The theorem holds whether the triangles lie in the same or in different planes.
-MORRIS KLINE
Mathematics in Western Culture (1953)

But I have resolved to quit only abstract Geometry, that is to say the research of questions that serve only to exercise the mind; this in order to have more leisure to cultivate another sort of Geometry, whose purpose is to explain questions about the phenomena of nature. If it pleases Desargues to consider what I've written about salt, about snow, about the rainbow etc., he knows well that all of my Physics is nothing other than Geometry.
-RENÉ DESCARTES
Letter to Mersenne (27 July 1638)

I undertake to prove that God, in creating the universe and regulating the order of the cosmos, had in view the five regular bodies of geometry as known since the days of Pythagoras and Plato, and that he has fixed according to those dimensions, the number of the heavens, their proportions, and the relations of their movements.
-JOHANNES KEPLER
Mystery of the Cosmos (1596)

It is my impression that the very special serenity of the starry sky is due to the geometrical relation of the stars to each other. -PIET MONDRIAN Natural Reality and Abstract Reality (1919-1920)

By way of analogy we can now say that although it is not possible to squeeze a four-dimensional body into a three-dimensional space without some parts sticking out, one can speak of the projections of various four-dimensional figures in our space of only three dimensions. But one must remember that just as the plane projections of three-dimensional bodies are two-dimensional or plane figures, so the projections of four-dimensional superbodies in our ordinary space will be represented by space-figures.
-GEORGE GAMOW
One, Two, Three, ... Infinity (1947)

	UP

BACK		NEXT

	HOME