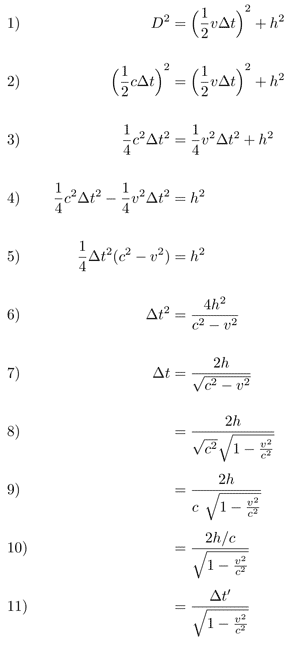Relativity
Einstein liked to think about things while riding on trains through the Alps. Europeans do not need a Disneyland. They have Switzerland.
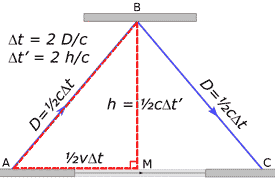
Sometimes, Einstein enjoyed bouncing a ball off the ceiling of the train. When the conductor glared at him, he just thought about it quietly to himself. One of the thoughts he had was: how would the ball look to someone outside the train watching him go by? So he drew a picture like the one above.
Let h be the height of the passenger car ceiling. Then to Einstein the ball would seem to go up and back down the distance of 2 × h while the train moved from point A to point C. To an observer outside the train, however, the ball would seem to travel from point A to B, and then down to C. To the outside observer, the distance the ball traveled would seem longer, just as the triangle shows.
When taking a trip, if we multiply our speed by the amount of time our trip takes, we can calculate the distance we travel. The formula you probably remember is d = v×t, where v is for velocity and t is for time elapsed. (From here on, we will put a Δ in front of t to mean elapsed time, which is the difference between two moments on our clock.) Notice also that the distance the train travels from A to C is vΔt, where v is the velocity or speed of the train, and Δt is the elapsed time according to the outside observer. In our diagram, the distance from A to M is ½vΔt.
The differences between inside and outside observations is only slight
if the train is moving slowly:

The slower the speed, the less distance from A to C, and therefore from A to M.
When the train stops,
the distances and times of inside and outside observers match.
However, if the train is moving rapidly,
the distance from A to M is greater:
![]()
Notice also that while the distance from A to M grows wider,
the distance from M to B shrinks accordingly.
Now replace Einstein with God. Assume that while God is flying by rapidly from A to C, he bounces a lightning bolt from his right hand at M to his left hand at B and back again. For us standing relatively still, the round trip distance of the lightning from one hand to the other (2×D = AB + BC) appears greater than it is for God (2×h = MB + BM). A little math shows that the time elapsed on our clocks Δt, as compared to the time elapsed on God's Timex Δt', is also greater.
By the triangle outlined in red dashes,
we know we can use the Pythagorean theorem to calculate God's time
Δt' if we know Δt, which is our time.
According to Pythagoras, (MB)² + (AM)² = (AB)².
Or, substituting our measurements,
h² + (½vΔt)² = D².
Using our equations, and a little algebra, let's solve for Δt.
Why? Because, from God's point of view, 2h = cΔt' is the roundtrip distance the bolt of lightning travels. Think about it... For more details, dig up your old Serway Physics text, and read Chapter 39 .